LARC(Latin America Regional Contests) 2018

https://www.acmicpc.net/category/detail/1956

Latin America Regional Contests 2018

www.acmicpc.net

22.09.16

전체 A~M 13문제 (FGIJK 제외 8솔)

아주 오랜만에 백준에서 문제를 풀었다.

최근 한 달간 한 것은 없지만 생각보다 바쁘게 살게 되었고, PS에 관심을 덜 가지게 되었다.

작년 ICPC 팀원들은 사정이 있어 올해 ICPC에는 참여하지 못하였고,

새로운 팀원 g3gogogo 그리고 cocjcr0208과 함께 하게 되었다.

새 학기 첫 연습으로 bnb2011 형님이 추천해준 셋 중 쉬운 셋을 골랐다.

첫 연습치고 괜찮은 결과지만 페널티 관리가 조금 아쉬웠다.

많이 연습을 진행해보고 공부하면 좋은 팀이 될 것 같아 기대된다.

A. A Symmetrical Pizza

문제

주어진 수(소수점 2자리까지 허용)에 임의의 수를 곱해서 360의 배수를 만들 수 있을 때, 가능한 수들 중 가장 작은 값을 구하여라

풀이

입력받은 수에 *100을 한 후 1~36000까지 돌면서 곱해보고 그 수가 36000으로 나누어떨어지는지 확인한다.

뭔가 더 간단한 풀이가 있을 것 같기는 하다.

소스코드

#include <bits/stdc++.h>
using namespace std;

int main(){
    int a, b;
    scanf("%d.%d",&a,&b);
    a=a*100+b;
    for(int i=1; i<=36000; i++){
        if(a*i%36000==0) printf("%d",i), exit(0);
    }
}

B. Building a Field

문제

원형으로 놓인 나무들이 있고 그 사이사이의 간격이 주어진다. 네 개의 나무를 골라 직사각형을 만들 수 있는지 구하라

풀이

모든 간격을 합한 값 S에 대해 S/2의 간격을 가진 두 나무 쌍이 2개 이상 있으면 직사각형을 만들 수 있다.

투포인터로 O(n)에 충분히 구해진다.

소스코드

#include <bits/stdc++.h>
using namespace std;
vector<int> v;
int n, c, s;
int main(){
    scanf("%d",&n); v.resize(n*2);
    for(int i=0; i<n; ++i) scanf("%d",&v[i]), v[i+n]=v[i], c+=v[i];
    if(c%2) puts("N"), exit(0);
    c/=2;

    int ch=0;
    for(int i=0, j=0; i<n; ++i){
        if(i) s-=v[i-1];
        for(;j<2*n && s<c; s+=v[j++]);
        if(s==c) ch++;
    }
    puts(ch>2?"Y":"N");
}

C. Cheap Trips

문제

주어지는 순서대로 여행을 갈 건데 120분 간격 안에서 시작되는 첫 여행은 100%, 두번째 여행은 50%, 3~6번째 여행은 25%, 그 이후는 다시 100%의 비용을 낸다. 여행의 첫 시작과 여행 사이사이에 딜레이를 자유롭게 줄 수 있을 때, 모든 여행에 드는 최소 비용은 얼마인지 구하라

풀이

g3gogogo가 해결했다.

7번째 이후의 여행은 모두 첫 여행으로 바꾸어 주면 된다. 각 여행에 대해 시작 딜레이(0~120)과 몇 번째 여행인지(1~6)을 기록해두는 DP를 이용하여 구하면 된다.

D. Database of Clients

문제

이메일을 받는데, 이메일의 local-part와 domain에 따라 사람을 구분할 수 있다.

local-part에서 두 가지 기준을 가진다.

- '.'은 무시한다.

- '+'이후의 문자열은 무시한다.

domain에서는 한 가지 기준을 따른다.

- domain이 다르면 다른 사람이다.

ex) bob@hello.com과 b.o.b@hello.com은 같은 사람이지만 bob@hellocom은 다른 사람이다.

이때, 주어진 이메일 주소들에서 다른 사람이 몇 명인지 구하여라

풀이

문자열 파싱을 잘 하면 된다..?

소스코드

#include <bits/stdc++.h>
using namespace std;
char S1[110], S2[110];
vector<pair<string,string>> mp;
int main(){
    int n;
    scanf("%d",&n);
    for(int i=0; i<n; ++i){
        scanf("\n%[^@]@%s",S1,S2);
        string s1, s2;

        for(int j=0; S1[j]; ++j){
            if(S1[j]=='.') continue;
            if(S1[j]=='+') break;
            s1.push_back(S1[j]);
        }
        for(int j=0; S2[j]; ++j) s2.push_back(S2[j]);
        mp.push_back({s1,s2});
    }
    sort(mp.begin(),mp.end());
    int c=1;
    for(int i=1; i<mp.size(); ++i){
        if(mp[i].first==mp[i-1].first && mp[i].second==mp[i-1].second) continue;
        ++c;
    }
    printf("%d",c);
}

E. Escape, Polygon!

문제

~~기하도망쳐!!~~

10^5각 이하의 볼록 다각형을 입력받는다. 다각형의 세 변을 직선으로 생각할 때, 직선들로 만들어진 영역에 대해 다음과 같이 구분할 수 있다.

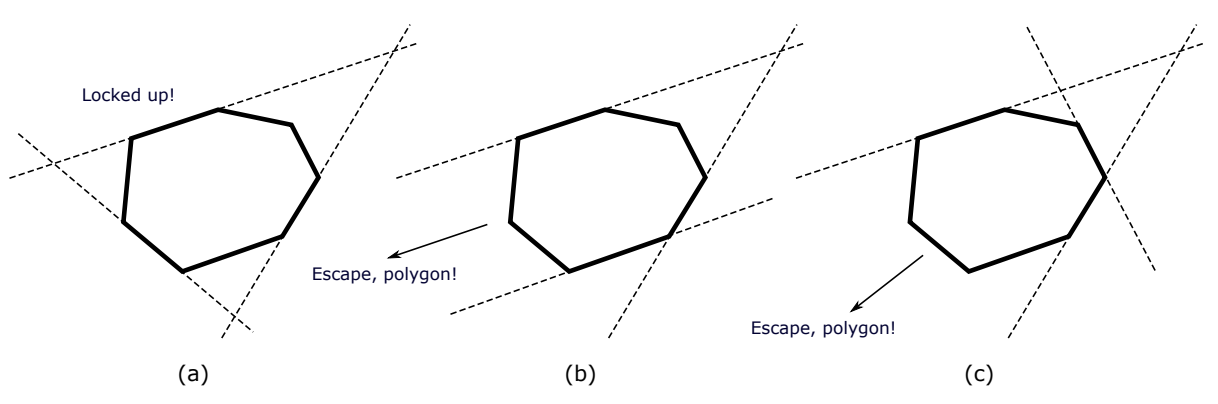
(a)는 다각형을 포함하며, (b), (c)는 다각형을 포함하지 못한다.

다각형을 포함하는 세 직선을 선택하는 방법의 수를 구하라

풀이

다각형의 임의의 변으로 만들 수 있는 직선을 x라 하자.

x'은 x와 평행한 점의 개수이다.

$v1_x$ 는 x~x'사이의 x'을 포함하지 않는 반시계 방향의 변 개수이다.

$v2_x$ 는 x~x'사이의 x'을 포함하는 반시계 방향의 변 개수이다.

$V_x$ 는 0~x사이의 변들에 대한 $v1_x$ 의 누적합이다.

특정 직선 A가 아래 변이라 가정하자. 만들 수 있는 삼각형의 개수는 다음과 같은 식으로 표현된다.

$ans = (V_{a+ v1_a + 1} - V_{a+1}) + (\frac {v1_a \times (v1_a - 1)} {2}) - (v1_a \times (v2_a - 1))$

모든 직선에 대해 해당 값을 누적한 후 3으로 나누어주면 답을 구할 수 있다.

소스코드

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pii;
const ll N = 2e5+10;
ll v[N], v2[N], V[N];
vector<pii> e;

ll ccw(pii a1, pii a2, pii b1, pii b2){
    b2.first = b2.first - b1.first + a2.first;
    b2.second = b2.second - b1.second + a2.second;
    auto&[x1,y1] = a1;
    auto&[x2,y2] = a2;
    auto&[x3,y3] = b2;
    ll temp = x1*y2+x2*y3+x3*y1 -y1*x2-y2*x3-y3*x1;
    if (temp > 0) return 1;
    else if (temp < 0) return -1;
    else return 0;
}

int main(){
    ll n;
    scanf("%lld",&n); e.resize(n*2+1);
    for(ll i=0; i<n; ++i){
        auto&[x,y] = e[i];
        scanf("%lld%lld",&x,&y); e[i+n] = e[i];
    } e[n*2] = e[0];

    for(ll i=0, j=1, j2=1; i<n; ++i){
        for(; j<2*n && ccw(e[i],e[i+1],e[j],e[j+1])>0; ++j);
        for(; j2<2*n && ccw(e[i],e[i+1],e[j2],e[j2+1])>=0; ++j2);
        v[i] = j-i-1;
        v2[i] = j2-i-1;
        if(i) V[i] = V[i-1] + v[i-1];
    }
    for(ll i=n; i<n*2; ++i) v[i] = v[i-n], V[i] = V[i-1] + v[i-1];

    ll pr=0;
    for(ll i=0; i<n; ++i) pr+=V[i+v[i]+1]-V[i+1] + v[i]*(v[i]-1)/2 - v[i] * (v2[i]-1);
    printf("%lld",pr/3);
}

F. Fantastic Beasts

문제

BAPC 2019의 Deck Randomisation과 비슷한 문제인 것 같다.

G. Gathering Red-Black Fruits

H. Highway Decommission

문제

최소가중치 다익스트라를 구하면 된다.

풀이

주어진 그래프에서 루트(노드 1번)과 모든 정점 사이의 최단경로를 이루는 간선을 구하되, 가능하면 최소 가중치 간선을 선택해야한다. pq를 사용하여 다익스트라를 잘 구현하면 해결할 수 있다.

소스코드

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N = 11000;
ll vis[N], d[N];
struct edge{ll p, l, c;};
struct cmp{
    bool operator()(edge &a, edge &b){
        return a.l>b.l || (a.l==b.l && a.c>b.c);
    }
};
vector<edge> e[N];
vector<edge> cnd[2];

ll pr;
int main(){
    ll n, m;
    scanf("%lld%lld",&n,&m);
    for(ll i=0; i<m; ++i){
        ll x, y, l, c;
        scanf("%lld%lld%lld%lld",&x,&y,&l,&c);
        e[x].push_back({y,l,c});
        e[y].push_back({x,l,c});
    }
    priority_queue<edge,vector<edge>,cmp> pq;
    vis[1]=1;
    for(ll now=1, vcnt=1; vcnt<n;){
        for(auto&[p,l,c]:e[now]){
            if(vis[p]) continue;
            pq.push({p,l+d[now],c});
        }
        while(!pq.empty()){
            auto [p,l,c] = pq.top(); pq.pop();
            if(vis[p]) continue;
            vis[p]=1; d[p]=l;
            now = p;
            pr+=c;
            ++vcnt;
            break;
        }
    }
    printf("%lld",pr);
}

I. https://www.acmicpc.net/problem/16529

문제

주어진 방향그래프에서 졸라맨을 최대 몇 개 그릴 수 있는지 구하여라

풀이

졸라맨은 머리 하나, 상체 하나(손 두 개&하체 한 개 달림), 하체 하나(발 두 개 달림)로 이루어져 있다.

실상 머리와 손, 발들은 같은 역할이므로 각 노드는 3개의 상태를 가질 수 있다.

1. 상체

2. 하체

3. 머리(혹은 손,발)

이를 잘 이용하여 tree에서의 dp를 구하면 되는데, 구현이 꼬여서 연습때는 해결하지 못했다.

J. Jeopardized Election

문제

V(odd)개의 길이 C의 sequence $S$ ( $S_i$ , $1 \leq i \leq C$ )가 주어진다.

임의의 길이 C인 sequence $A$ 를 하나 만들어보자.

$A_1$ 부터 시작하여 다음의 작업을 반복한다.

1. $S$ 들의 첫 자리가 $A_i$ 인 케이스의 수 C'에 대해 $C' < C/2$ 라면 $S$ 들에서 $A_i$ 를 모두 지운다.

2. $C' > C/2$ 라면 해당 값 ANS을 선택 후 종료한다.

원하는 ANS가 선택되도록 $A$ 를 만들어라

K. https://www.acmicpc.net/problem/16531

문제

N개의 수가 있다. 이를 잘 조합하여 $2^N$ 개의 수들을 얻었다.

우리는 이 $2^N$ 개의 수를 알 때, 원래의 N개 수를 구해야 한다.

풀이

모두 합했을 때, $2^{N-1}\times (모든 수의 합)$ 임을 알 수 있다.

그리고, 모르겠다 :)

L. Looking for the Risk Factor

문제

Q개의 쿼리가 주어진다. 각 쿼리는 두 개의 수 N과 K로 이루어지는데,

2 이상 N 이하의 수들 중 K보다 작은 인수들로만 이루어진 수의 개수를 구해야 한다.

풀이

오프라인 쿼리 문제이다.

에라토스테네스의 체로 전처리O(NlogNlogN)를 한 후,

모든 값들에 대해 자신의 가장 큰 소인수에 해당하는 벡터에 기록한다.

쿼리에 들어온 값 이하의 모든 소인수들에 대해 이분탐색으로 개수를 구한다.

수행시간이 1.7초인 것을 보아 정해는 아니지만, 충분히 잘 돌아가는 해답인 것 같다.

소스코드

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int chk[N], no;
vector<int> insu[N];
map<int,int> mp;
vector<vector<int>> vec;
int main(){
    mp[2]=no++;
    for(int j=2; j<N; j+=2) chk[j]=1, insu[j].push_back(2);
    for(int i=3; i<N; ++i){
        if(chk[i]) {mp[i] = no-1; continue;}
        mp[i]=no++;
        for(int j=i; j<N; j+=i) chk[j]=1, insu[j].push_back(i);
    }
    vec.resize(no);
    for(int i=2; i<N; ++i) vec[mp[insu[i][insu[i].size()-1]]].push_back(i);
    
    int T;
    scanf("%d",&T);
    for(int n, k; T--;){
        int p=0;
        scanf("%d%d",&n,&k);
        for(int j=mp[k]; j>=0; --j){
            p+=upper_bound(vec[j].begin(),vec[j].end(),n)-vec[j].begin();
        }
        printf("%d\n",p);
    }
}

M. Mount Marathon

문제

무언가 쉬운 문제였다고 한다.

풀이

cocjr0208씨가 해결하였다.

저작자표시 비영리

'PS > BOJ' 카테고리의 다른 글

NWERC(Northwestern Europian Regional Contest) 2021 (0)	2022.10.01
NANC(North Central North America) 2020 (4)	2022.09.25
SWERC 2018 (0)	2022.07.11
GCPC 2020 (0)	2022.05.25
BAPC 2021 (0)	2022.05.09

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

심심하다

LARC(Latin America Regional Contests) 2018

A. A Symmetrical Pizza

B. Building a Field

C. Cheap Trips

D. Database of Clients

E. Escape, Polygon!

F. Fantastic Beasts

G. Gathering Red-Black Fruits

H. Highway Decommission

I. https://www.acmicpc.net/problem/16529

J. Jeopardized Election

K. https://www.acmicpc.net/problem/16531

L. Looking for the Risk Factor

M. Mount Marathon

'PS > BOJ' 카테고리의 다른 글

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역

LARC(Latin America Regional Contests) 2018

A. A Symmetrical Pizza

B. Building a Field

C. Cheap Trips

D. Database of Clients

E. Escape, Polygon!

F. Fantastic Beasts

G. Gathering Red-Black Fruits

H. Highway Decommission

I. https://www.acmicpc.net/problem/16529

J. Jeopardized Election

K. https://www.acmicpc.net/problem/16531

L. Looking for the Risk Factor

M. Mount Marathon

'PS > BOJ' 카테고리의 다른 글

'PS/BOJ' Related Articles

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역