 Relations and Functions
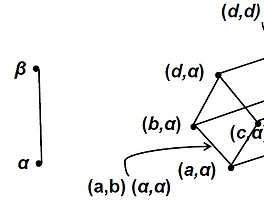
중간고사 이전 부분은 Set/Propositions, Permutation/Combination/Discrete probability이나 pass함 Relations and Funcitons Intruduction Cartesian product of A and set B, A x B : set of all ordered pairs (a,b) where $a \in A$ and $b \in B$ ex) {a, b} x {a, c, d} = {(a,a), (a,c), (a,d), (b,a), (b,c), (b,d)} Binary relation from set A to set B : - subset of A x B - R is binary relation from A to B and if (a,b) $\i..
Relations and Functions
중간고사 이전 부분은 Set/Propositions, Permutation/Combination/Discrete probability이나 pass함 Relations and Funcitons Intruduction Cartesian product of A and set B, A x B : set of all ordered pairs (a,b) where $a \in A$ and $b \in B$ ex) {a, b} x {a, c, d} = {(a,a), (a,c), (a,d), (b,a), (b,c), (b,d)} Binary relation from set A to set B : - subset of A x B - R is binary relation from A to B and if (a,b) $\i..